Teljesítményelektronikai ötletek – 10
Megjelent: 2012. március 05.
 Előfordul, hogy a fejlesztőmérnök komoly eltérést tapasztal elméleti számításai és a labormérések eredményei között. Ilyenkor el lehet gondolkodni, hogy „elszámítottunk”, esetleg „elmértünk-e” valamit. A hibakeresésben, szakszerűen szólva a veszteségforrások identifi kációjában segít Robert Kollman sorozatának e havi folytatása.
Előfordul, hogy a fejlesztőmérnök komoly eltérést tapasztal elméleti számításai és a labormérések eredményei között. Ilyenkor el lehet gondolkodni, hogy „elszámítottunk”, esetleg „elmértünk-e” valamit. A hibakeresésben, szakszerűen szólva a veszteségforrások identifi kációjában segít Robert Kollman sorozatának e havi folytatása.
Tápegység-áramkörök veszteségének számítása
Megtörtént-e már az olvasóval, hogy újra és újra ellenőrizte a számításait, amikor egy teljesítmény elektronikai áramkör számított vesztesége „köszönő viszonyban” sem volt a labormérések eredményével? Ez a cikk egyszerű módszert mutat be az ilyesfajta eltérések felderítésére. A módszer a Taylor-sorfejtésen alapul, amely szerint – gyakorlatilag – minden függvény felírható polinomalakban az alábbiak szerint:

Ha egy tápegység veszteségeit a kimeneti áram függvényeként vizsgáljuk, a fenti kifejezésben az x helyére a kimeneti áramot kell írnunk. Felismerhetjük, hogy ez esetben a polinom együtthatói szoros összefüggésben vannak a teljesítményveszteség különböző forrásaival. Például a0 jelképezi azokat a fix teljesítményveszteségeket, amelyek függetlenek a terhelőáramtól. Ilyenek a kapumeghajtó és a segéd-tápfeszültség okozta veszteségek, vagy a teljesítménytranzisztor kapuelektróda-kapacitásának töltése és kisütése közben fellépő veszteség. Ezek a veszteségek függetlenek a kimeneti áramtól.
A polinom második tagjában szereplő a1 együttható azokra a veszteségekre jellemző, amelyek egyenesen arányosak a kimeneti árammal. Ilyenek a kimeneti dióda veszteségei és a kapcsolási veszteségek. A kimeneti dióda veszteségét jórészt az aktív réteg nagyjából állandó feszültségesése okozza, ezért ez a veszteség egyenesen arányos a diódán is átfolyó kimeneti árammal. Hasonlóképpen a kapcsolási veszteségekre is az jellemző, hogy a kimeneti áram és valamilyen állandó feszültség szorzataként számítható.
A Taylor-polinom harmadik tagja (a2x2) könnyen azonosítható a vezetési veszteségekkel. Ezek közé tartozik jellegzetesen a kapcsolófet, az induktív elemek és az alkatrészek közötti huzalozás ellenállásán keletkező veszteség.
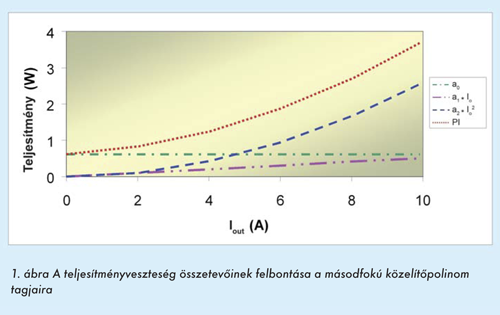
Az ennél magasabb rendű tagok az olyan nemlineáris komponensek értékelésénél lehetnek hasznosak, mint például a vasveszteség, amely az induktivitás vasmagjában keletkezik, ám igazán jó eredményeket csak a polinom első három tagjától (a0 , a1x és a2x2) várhatunk.
A három tag együtthatóinak meghatározásának egy lehetséges módszere, hogy három munkapontban (háromféle terhelőáramnál) végzünk veszteségmérést és megoldjuk az így adódó háromismeretlenes egyenletrendszert. A megoldás tovább egyszerűsíthető, ha az egyik mérést terheletlen állapotban végezzük: ez esetben ugyanis a veszteség közvetlenül a Taylor-sor első tagját, az a0-t adja. Ezzel a probléma két egyenletből álló, kétismeretlenes egyenletrendszerre egyszerűsödik, amely már egészen könnyen megoldható. Miután az együtthatókat kiszámítottuk, az 1. ábrához hasonló veszteségiteljesítmény-diagram adódik, amely külön mutatja a háromféle veszteségtípus függését a kimeneti áramtól. Ez nagyon hasznos lehet a mérések és számítások eredményei közötti különbségek okainak felderítésénél, de segítségünkre lehet abban is, hogy megtaláljuk a potenciális hatásfokjavítási lehetőségeket. Például az 1. ábrán látható esetben, teljes terhelésnél a veszteségnek az „ohmos” (az ellenállásokon eső feszültség által okozott) összetevő a domináns meghatározója. Az ilyen esetben tehát a hatásfokjavításhoz kisebb bekapcsolási ellenállású kapcsolófetet érdemes választani, vagy az induktív tekercset alkotó vezeték, esetleg az alkatrészek közötti huzalozás keresztmetszetét kell növelni.
A tényleges veszteség és a háromtagú Taylor-polinommal leírt veszteségfüggvény között nagyon szoros a korreláció. A 2. ábra mutatja a mért adatok és a Taylor-polinommal három pontra végzett görbeillesztéses függvényközelítés összehasonlítását egy szinkron feszültségcsökkentő feszültségszabályozó esetében. Tudjuk, hogy ezek három kimeneti áramértéknél (a háromismeretlenes egyenletrendszer gyökhelyeinél) pontosan egyeznek. A többi szakaszon az eltérés a mért értékek és a Taylor-polinom első három tagjával leírt közelítő függvény között mindenütt kisebb 2%-nál. Másfajta tápegységeknél előfordulhat ennél kevésbé pontos egyezés, amelynek oka a másféle működési mód (folyamatos vagy szakaszos, impulzuskihagyásos vagy változó frekvenciájú működés). A módszer tehát nem csalhatatlan, ám mindenképpen hasznos hozzájárulást jelent a tápegységtervezőnek a tényleges áramköri veszteségek okainak elemzéséhez.
Következő havi számunkban Robert Kollman bemutatja, hogyan lehet ezt a módszert felhasználni a hatásfok egy bizonyos munkapontban történő optimalizálására.
www.power.ti.com
http://www.ti.com/ww/hu/cikkek-szakirodalom.html
A cikksorozat korábbi részei:
1. rész |
2. rész |
3. rész |
4. rész |
5. rész |
6. rész |
7. rész |
8. rész |
9. rész |
|





 Robert Kollman, a Texas Instruments műszaki állományának kiemelt tagja, vezető alkalmazástechnikai mérnök. Több mint 30 év tapasztalattal rendelkezik a teljesítményelektronikában és egy ideig induktív alkatrészeket tervezett az 1 W alattitól a csaknem 1 MW-ig terjedő teljesítménytartományú elektronikus áramkörökhöz, egészen a megahertzes kapcsolási frekvenciákig. Robert Kollman a Texas A&M Egyetemen BSEEdiplomát, majd a Déli Metodista Egyetemen Master-fokozatot (MSEE) szerzett. A cikksorozattal kapcsolatban a
Robert Kollman, a Texas Instruments műszaki állományának kiemelt tagja, vezető alkalmazástechnikai mérnök. Több mint 30 év tapasztalattal rendelkezik a teljesítményelektronikában és egy ideig induktív alkatrészeket tervezett az 1 W alattitól a csaknem 1 MW-ig terjedő teljesítménytartományú elektronikus áramkörökhöz, egészen a megahertzes kapcsolási frekvenciákig. Robert Kollman a Texas A&M Egyetemen BSEEdiplomát, majd a Déli Metodista Egyetemen Master-fokozatot (MSEE) szerzett. A cikksorozattal kapcsolatban a 












