A radartechnika alapjai 2. rész - A működési elv

Sorozatunk első részében áttekintettük a mai radar megjelenéséhez vezető technikatörténeti folyamatot. Bár a kezdetektől napjainkig nagy változásokon ment át a radar technikai kivitele, és hihetetlenül kibővült az alkalmazási köre, az alapelve azonos. A második részben az alapelvvel foglalkozunk.

A legegyszerűbb radarok alapelve könnyen érthető, bár az elméleti háttere meglehetősen komplex. Az elmélet bizonyos fokú megértése viszont feltétlenül szükséges ahhoz, hogy akár csak egy egyszerű radarrendszert specifikáljunk vagy üzemeltessünk. A megvalósítás és üzemeltetés számos olyan műszaki szakterületet érint, mint az építészet, a nagy teherbírású, precíziós mechanikai szerkezetek, az erősáramú elektrotechnika és ipari elektronika, a nagy teljesítményű mikrohullámú jelek előállítása, valamint a nagy sebességű jel- és adatfeldolgozás és megjelenítés. Az alapelvek megértéséhez azonban csak néhány természeti törvény ismeretére van szükségünk.

A távolság radarelvű mérése az elektromágneses hullámok tulajdonságain alapul. Ezek a következők:

• Az elektromágneses hullámok akkor verődnek vissza, ha elektromosan vezetőképes felülettel találkoznak. Ha ezeket a visszavert hullámokat a kibocsátás helyén detektáljuk, az azt jelenti, hogy a kisugárzás irányában elektromágneses hullámokat visszaverő tárgy található.

• Az elektromágneses energia a levegőben állandó sebességgel terjed, amely jó közelítéssel azonos a fény vákuumbeli terjedési sebességével (kb. 0,3%-kal kisebb annál)^[1] . Egyszerű számításoknál megszokott a 300 000 km/s értékkel való közelítés. A fénysebesség állandósága lehetővé teszi a radarberendezés és egy reflektáló tárgy (repülőgép, hajó, gépkocsi) távolságának (az 1. ábrán R_S) meghatározását. A távolságmérést a kibocsátott és visszavert hullám terjedési idejének mérésére vezetjük vissza. A mérés bizonytalanságát csak az atmoszférikus és időjárási feltételek bizonytalansága okozza (természetesen a technikai megvalósításból adódó bizonytalansággal együtt).

• Az elektromágneses energia elvileg egyenes vonalban terjed, amelyet csak kismértékben befolyásolnak az atmoszférikus és időjárási tényezők. Speciális radarantennák segítségével a kibocsátott elektromágneses hullámot a kívánt irányba fókuszálják. A radarantenna maximális visszavert jelet adó pozíciójának megkeresésével a visszaverő objektum azimutja (oldalszög, az 1. ábrán AZ) és elevációja (emelkedési szög, az 1. ábrán EL) meghatározható.

1. ábra

Távolságmeghatározás

A radar egy rövid, nagy teljesítményű impulzust bocsát ki. Ezt az impulzust az antenna irányhatásával erősen fókuszálják, és az az antennától a fény sebességével távolodik. Ha ebben az irányban egy elektromosan vezető anyagú tárgy (céltárgy – például egy repülőgép) található, az antenna által kibocsátott energia legnagyobb része a térben szétszóródik. Egy nagyon kis energiahányad azonban éppen a radar irányába verődik vissza. A radarantennában ez az elektromágneses energia villamos jelet hoz létre, és a radar értékeli az ebből származtatható információt.

Mit is jelent a távolság?
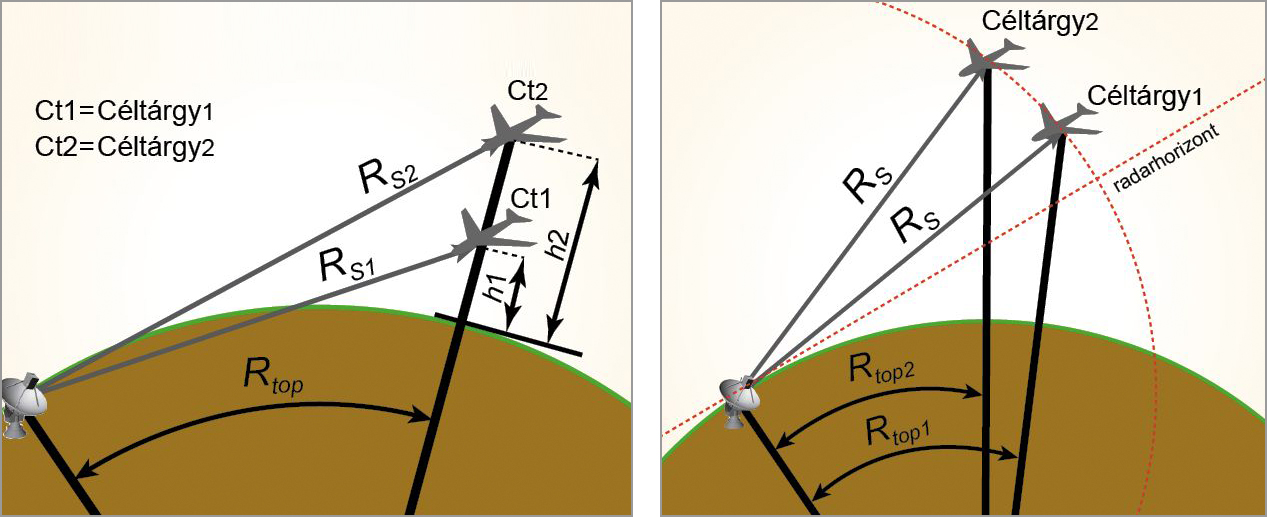
A „távolság” fogalma a radartechnikában bizonyos pontosításra szorul. Könnyen érthető, de a félreértés elkerülése miatt mégis megjegyezzük, hogy a radar az antenna és a céltágy közötti „látóirányú” egyenes vonal menti távolságot (a továbbiakban a nemzetközileg egységesen értelmezett angol „slant range” kifejezést használjuk, és az ábrákon R_S-el jelöljük) méri, nem pedig a radar földrajzi helye és a céltárgy földfelszínre vetített pontja közötti (R_top) földrajzi (topográfiai) távolságot („down range”). Ez például azzal jár, hogy a földfelszín azonos pontja felett, tehát azonos topográfiai távolságban, de különböző magasságban elhelyezkedő két céltárgy radarral mért távolsága különböző (2a, 2b ábra). Modern radarberendezésekben – a korszerűtlen, 2D-típusokkal ellentétben – olyan szoftvermodul található, amely elvégzi a földfelszínre vetítés műveletét, figyelembe véve a céltárgy magasságát és a földfelszín görbületét is. Ez a számítás meglehetősen bonyolult, és bizonyos időjárási adatok ismeretét is megkívánja.
A „slant range” távolságot akár egy egyszerű oszcilloszkóppal is megmérhetjük. Az oszcilloszkóp vízszintes eltérítését a kibocsátott radarimpulzus indítja, és a kijelzőn egy fénypont indul balról jobbra az eltérítés állandó sebességével. Ezért a megjelenített kép bal szélén látható a kibocsátott, nagy amplitúdójú impulzusjel. Amikor az antenna érzékeli a visszavert (a kibocsátottnál jóval kisebb) jelet, az az oszcilloszkóp-képernyőn egy kisebb impulzusként jelenik meg. A képernyőn a két impulzus között mérhető távolság arányos a radar és a céltárgy távolságával.
Mivel a rádióhullámok állandó sebességgel (a c fénysebességgel) terjednek, a céltárgy és a radar közötti távolság az impulzus terjedési idejéből kiszámítható.
A „slant range” (R_S) számítása egyszerű: R_S = c · t/2, ahol c a fénysebesség (≈300 000 km/s), t a visszavert és kibocsátott jel időkülönbsége. A kettes faktort a nevezőben azért kell alkalmaznunk, mert t idő alatt a c sebességű hullám „oda-vissza” kétszer teszi meg az R_S távolságot.

2a ábra és 2b ábra

Iránymeghatározás

A távolságméréssel egyidejűleg a céltárgy oldalirányú (azimut) és magassági (eleváció) szöge is meghatározható. Ehhez irányított antennára van szükség, amely a kibocsátott energiát nagymértékben nyalábolja, azaz tengelyirányban sokszorta nagyobb, más irányokban sokkal kisebb energiát bocsát ki és érzékel, mint egy minden irányban egyforma energiasűrűségű „gömbsugárzó”. Az irányítottság mértéke az antennanyereség fogalmával, valamint az alkalmazott frekvenciától is függ: adott méretű antennával, nagyobb frekvenciájú jelet használva nő az antennanyereség, illetve egy adott nyereségű (és irányítottságú) antennát kisebb méretben is meg lehet valósítani. A nagyobb üzemi frekvencia előnye még a fényhullámokhoz hasonló, egyenes vonalú, kis elhajlású terjedés, a nagy felbontás (a nagyobb frekvenciájú – kisebb hullámhosszú – jel kisebb tárgyakról is jobban visszaverődik).

3. ábra

A céltárgy irányának meghatározásához az antenna sugárzási tengelyét kell a céltárgy irányába fordítani. Ehhez feltételezzük, hogy az antenna egy függőleges és egy vízszintes tengely körül elfordítható. A függőleges tengely körüli elfordulást (azimut – AZ) az óramutató járása irányában növekvő, 0…360° tartományú szöggel jellemezzük, amelynek a kezdőpontja az északi irány. Ehhez a radart telepítéskor az északi irányhoz tájolni kell. Régebbi berendezéseknél ezt ismert tereppontokhoz viszonyítva vagy mágneses tájolóval végezték. Ma ezt GPS-eszközökkel végzik, a mágneses és topológiai északi irány közötti helyfüggő eltérések kiküszöbölésével. A magassági szög (eleváció – EL, ε) mérése a horizont síkjához viszonyítva történik, maximális értéke 90°. Magas telepítési helyeken, ahol a horizont „alá” is lát a radar, az eleváció negatív értéket is felvehet.
A radar üzemeltetőjét nem elsősorban a radar és a céltárgy közötti „egyenes” távolság, a „slant range” érdekli, hanem a céltárgynak a felszínre vetített távolsága, a „down range”. Ennek segítségével képes például a radar – az elvárható legnagyobb pontossággal – egy elektronikusan generált térképen megjeleníteni a céltárgy helyét. A céltárgy földfelszín feletti pontos magasságának kiszámítására tekintsük a 3. ábrát. Ezen az RCT_K háromszög azt jelképezi, hogyan számítanánk ki a céltárgynak a síknak tekintett földfelszín feletti magasságát (mivel ez a valódi H magasság közelítése, nevezzük H_K-nak) és a topológiai távolságát (R_topK). Ehhez a radarmérésből ismert az R_S és az ε, amelyekkel H_K = R_S sin ε, továbbá R_topK = R_S cos ε. A radar telepítési helyéből ismert továbbá annak a Föld középpontjától mért távolsága (r_e). Keressük a céltárgy valódi magasságát (a céltárgynak (C) a földfelszíni vetületétől (T) mért merőleges távolságát), valamint a radar (R) és a T pont közötti r_e sugarú ív hosszát, amely a radar és a céltárgy valódi topológiai távolsága (R_top).
Elsőként határozzuk meg az RCF háromszög CF oldalát, ami H és az ismert r_e összege, amiből a H az egyik keresett érték. Ehhez kiszámíthatjuk a C-nél levő γ szög értékét: γ = 90° - (ε + α). Kiszámítható az R pontnál levő ρ szög értéke is: ρ = 90 °+ ε. Most tehát az RCF háromszögnek ismert két oldala (R_S és r_e) és az általuk bezárt szög (ρ). A keresett CF oldal (r_e+H) hosszúsága a koszinusztétellel számítható a következőképpen:
, amelyből

Most már kiszámítható az α szög is az RCF háromszögre felírt szinusztételből:

tehát,

Az α ismeretében pedig számítható R_top, azaz a C és T közötti r_e sugarú ív hossza is:

Az R_top és H értéke a valódi földrajzi távolságnak még mindig csupán a közelítése, mivel a radar által kibocsátott elektromágneses hullám a légkörön áthaladva a fénytöréshez hasonló irányváltozást szenved. Emiatt a háromszögnek az R_S távolsággal jelölt oldala nem egyenes, hanem az alábbiaktól függő mértékben elhajlik:

• a radar által sugárzott jel hullámhossza,

• a barometrikus nyomás,

• a levegő hőmérséklete és

• nedvességtartalma.

Ennek következtében a radar térképes megjelenítése pontatlan, ha a radar számítógépe ezeket a – csak részben pontosan ismerhető – körülményeket nem veszi figyelembe.

Készítette: Tóth Ferenc a www.radartutorial.eu weblap (szerző: Christian Wolff) fordításával és átdolgozásával, a GNU Free Documentation License és a Creative Commons „Nevezd meg – Így add tovább 4.0” licence alapján.

A cikksorozat korábbi részei:

[1]A fény vákuumbeli terjedési sebessége (c_vákuum) 299 792 458 m/s. Ez a mai értelemben nem mérési eredmény, hanem az SI-mértékrendszer összefüggéseit meghatározó, 1975-ben egyezményesen rögzített értékű fizikai állandó. (A méréselmélet fejlődésének különös „vargabetűje”, hogy a fény sebességét eredetileg az egységnyi hosszúság és idő egyezményes értékeinek felhasználásával mérték meg. Az 1975-ben egyezménybe foglalt méréselméleti szemléletváltás óta azonban a fény vákuumbeli sebességét definiáljuk alapmennyiségként, a távolságegység definícióját ebből és az időegység atomi rezgésen alapuló definíciójából származtatjuk. Ha tehát valaki az eddiginél pontosabban méri meg a fénysebességet, azzal lényegében a méter definícióját pontosítja). Átlátszó közegekben a fény sebessége azok törésmutatójától függ (c_közeg = c_vákuum / törésmutató). Mivel a relatív törésmutató mindig nagyobb 1-nél, a fény sebessége bármilyen „nem vákuum” közegben kisebb a c_vákuum értéknél. A levegő törésmutatója közelítőleg 1,003, pontos értéke a levegő fizikai állapotától függ. Ezért a fény terjedési sebessége levegőben (a c_levegő = c_vákuum / 1,003 képlettel számítva) kb. 2,989×10⁸ m/s-nek adódik.