A radartechnika alapjai 10. rész – Van másmilyen moduláció is
Az év elején indult radartechnikai sorozatunk tizedik – terveink szerint az utolsó – részéhez ért. „Befejező” résznek mégsem nevezhetjük, mert a radar nem nevezető „megállapodott” technológiának. Inkább új kihívásokkal szembesül, hiszen például az autóiparban éppen most áll egy szinte felbecsülhetetlen méretű piac kapujában. A témát tehát inkább csak abbahagyjuk, de előbb még „elvarrunk néhány szálat”.
Sorozatunk eddigi részeiben szinte kizárólag az impulzusradarokkal foglalkoztunk. Ennek elsősorban az az oka, hogy a vezérfonalként és forrásmunkaként felhasznált webes „tankönyvet” érezhetően egy, a repülés (és talán ezen belül is a katonai repülés) területén dolgozó szakember készítette, és erre az alkalmazási területre főként az impulzusmodulált radarok alkalmazása a jellemző. Hiba lenne azonban a sorozatot úgy lezárni, hogy ne ejtenénk szót néhány más alkalmazási területről is. Ezek közül említsünk elsőként egy olyan technológiát, amely egy közismert, hétköznapi jelenséget ültet át a radartechnika környezetébe.
A Doppler-radar
Mindannyian tapasztaltuk már, ahogy egy hozzánk közeledő mentőautó szirénájának hangmagassága hirtelen mélyebbé válik, amikor a jármű elhalad mellettünk és távolodni kezd. A jelenség magyarázatát és kvantitatív leírását Christian Doppler osztrák fizikus publikálta elsőként 1842-ben. A megfigyelő felé mozgó hangforrás által kibocsátott hanghullámok rövidülnek, mert a hullámfrontok megérkezése közben a hangforrás is közeledik hozzánk – a megfigyelt hullámok „sűrűsödnek”, a nyugvó hangforráséhoz képest magasabb hangot hallunk. Távolodáskor pedig fordított jelenséget észlelünk. A „matek” részletezése nélkül a Doppler-effektus miatt megváltozott frekvencia (f):

ahol c a hullám terjedési sebessége az adott közegben, vf a hullámforrás sebessége (pozitív, ha a hullámforrás közeledik a megfigyelőhöz), vm pedig a megfigyelő sebessége (pozitív, ha a hullámforrás távolodik a megfigyelőtől), f0 a hullámforrás frekvenciája. A frekvencia tehát növekszik, ha a hullámforrás közeledik a megfigyelőhöz. (A pontosság kedvéért: a hullámforrás és a megfigyelő sebessége alatt a sebességnek a forrást a megfigyelővel összekötő egyenessel párhuzamos komponensét kell érteni.[1]) A Doppler-effektus számos alkalmazása között említjük a véráramlás sebességét mérő ultrahangos készüléket, a csillagászatban a csillagok, galaxisok radiális sebességének mérését a vöröseltolódás alapján, a rendőrség kézi radaros sebességmérőjét („radarpisztoly”), és az időjárási radarokat.
A legegyszerűbb Doppler-radar folytonos és modulálatlan elektromágneses hullámot (Continuous Wave – CW) bocsát ki a mozgó céltárgy irányába, és a visszavert hullám frekvenciájának eltolódásából kiszámítható a mozgó tárgy és a megfigyelő egymáshoz viszonyított (relatív), és a radart a céltárggyal összekötő egyenessel párhuzamos (radiális) sebességkomponense. A kibocsátott és a visszavert jel frekvenciájának külön-külön megmérése és az eredmények különbségének számítása elvileg járható út, de a különbségi (Doppler) frekvenciát a gyakorlatban inkább nemlineáris elektronikus eszközzel (keverő, szorzó) állítják elő. Ismét más módszer a frekvenciaeltolódás kiolvasása a visszavert jel Fourier-transzformációval (FFT[2]) előállított frekvenciaspektrumából. Mivel a mért sebesség rendszerint elhanyagolható a radarhullám terjedési sebességéhez (a fénysebességhez) képest, egyszerűsítésekre van lehetőség. A frekvenciaeltolódás ismeretében a sebesség  [1] ahol fD a Doppler-frekvencia, fa az adó vivőfrekvenciája és c a fénysebesség. Itt jegyezzük meg, hogy az ötlet az impulzusradaroknál is kihasználható. Ugyanis ha a radaradó periodikus impulzussorozatot bocsát ki, a reflektált jelsorozat impulzusfrekvenciája is a Doppler-effektusnak megfelelően változik (Coherent Pulse – CP-radar). Mivel egy impulzussorozat frekvenciája digitális technikával igen jól mérhető, a CP-radar meglehetősen elterjedt a gyakorlatban. A CW-radar mellett szól az is, hogy nincs szükség nagyteljesítményű impulzusok előállítására (kis tápegység, kisteljesítményű adóerősítő), ezért ez pehelykönnyű, kicsi és keveset fogyaszt az impulzusradarokhoz képest.
[1] ahol fD a Doppler-frekvencia, fa az adó vivőfrekvenciája és c a fénysebesség. Itt jegyezzük meg, hogy az ötlet az impulzusradaroknál is kihasználható. Ugyanis ha a radaradó periodikus impulzussorozatot bocsát ki, a reflektált jelsorozat impulzusfrekvenciája is a Doppler-effektusnak megfelelően változik (Coherent Pulse – CP-radar). Mivel egy impulzussorozat frekvenciája digitális technikával igen jól mérhető, a CP-radar meglehetősen elterjedt a gyakorlatban. A CW-radar mellett szól az is, hogy nincs szükség nagyteljesítményű impulzusok előállítására (kis tápegység, kisteljesítményű adóerősítő), ezért ez pehelykönnyű, kicsi és keveset fogyaszt az impulzusradarokhoz képest.
Folytonos hullámú, frekvenciamodulált (CWFM) radar
Az egyszerű Doppler-radar csak sebességet képes mérni, ám egy kis rendszertechnikai „ráfejlesztéssel” a (relatív, radiális) sebességen kívül a távolságot is meg tudjuk határozni a CW-radarhoz hasonlóan egyszerű, kisméretű és és olcsó berendezéssel. Ez rendkívüli előny azoknál a kis hatótávolságú radaroknál, amelyeket például épp most kezdenek szélesebb körben alkalmazni a vezetéstámogatásra (Advanced Driver Assistance System – ADAS) vagy éppen önvezetésre képes autókban, ahol a távolság és a relatív sebesség egyidejű ismerete egyaránt létfontosságú. Lássuk először, hogyan méri a CWFM-radar a hozzá képest nyugvó céltárgy távolságát.
Egy radarjel a céltárgyról Δt = 2R/c [2] idő alatt verődik vissza. Legyen a radarjelünk egy fűrészjellel modulált frekvenciájú szinuszhullám, amelynek frekvenciája T idő alatt Δf értékkel változik. (Az ehhez hasonlóan változó frekvenciájú hang „csiripelésre” hasonlít – nem véletlen, hogy angolul is „chirp”-nek nevezik.) Mint azt láttuk, ez a jel Δt idő múlva visszaérkezik az adóhoz. Ha a kibocsátott jel, valamint a reflektált, felerősített jel különbségét képezzük (fk) (például egy keverő segítségével), akkor az 1. ábrából[3]az alábbiakat írhatjuk fel: azaz
azaz
a Δt jelterjedési időt behelyettesítve .
.

Ebből az R távolság:  [3].
[3].
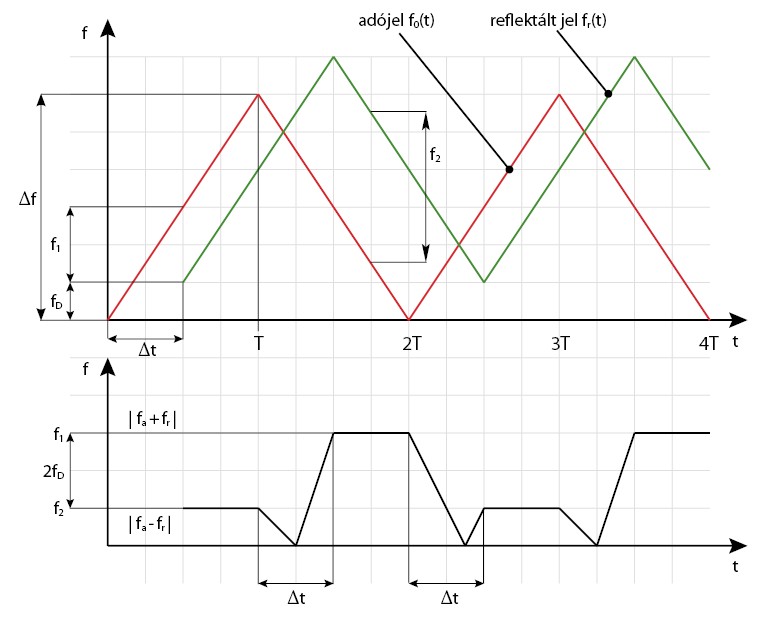
Ha viszont a céltárgy és a radar relatív radiális sebessége nem nulla (ami autóradarnál elég ésszerű feltételezés), a reflektált jel frekvenciáját a Doppler-hatás is módosítja. Moduláljuk az adó frekvenciáját most egy szimmetrikus háromszögjellel a 2. ábra szerint! Hogy az előbbi példával összehasonlíthassuk, T-vel ennek félperiódus-idejét jelöljük. A radarhoz képest radiálisan elmozduló céltárgyról reflektált jel fD frekvenciával elcsúszik a frekvenciatengely mentén a Doppler-hatás miatt. Emiatt az adó vivőjele (fa(t)) és a reflektált jel (fr(t)) közötti fa(t) – fr(t) különbségfüggvény minden periódusának lesz két időben állandó szakasza (lásd a 2. ábra alsó idődiagramját. Vegyük észre, hogy a különbségi frekvencia abszolút értékét ábrázoltuk – a negatív frekvencia itt nincs értelmezve.) Könnyen belátható, hogy az f1 és f2 különbségének abszolút értéke az fD Doppler-frekvencia kétszerese –, amelyből az
[1] képlettel a v sebesség kiszámítható:
Az R távolság kiszámításához vegyük figyelembe, hogy a 2. ábrából kiolvashatóan a T félperiódus-idő és a Δt terjedési késleltetés aránya azonos az adó teljes frekvenciaváltozásának (Δf-nek), valamint az fD Doppler-frekvencia és az f1 frekvencia összegének
arányával, tehát  .
.
Ebből helyettesítés után,
helyettesítés után,
a terjedési időt kifejezve adódik.
adódik.
Ezt a [2] egyenletbe helyettesítve a távolságra
az képletet kapjuk.
képletet kapjuk.
Megjegyezzük még, hogy a CWFM-radar bizonyos továbbfejlesztése a „képalkotó radar” (imaging radar), amely a távérzékelésben tett szert különleges jelentőségre, de ez már meghaladja sorozatunk kereteit.
Zárszó
A 2016. évi első számunkban indított radartechnikai sorozatunk utolsó részéhez ért. Nem hinném, hogy a sorozat cikkeit olvasva bárki radartechnikussá képezhette magát, jómagam is megmaradtam érdeklődő laikusnak. Be kell vallanom, úgy jártam, mint az 1950-es évek „átképzett” orosztanárai, akik egy leckével jártak a tanítványaik előtt. A sorozatot még sokáig lehetne folytatni, de megriadtam attól, hogy a vártnál – számomra – szövevényesebbnek bizonyult téma már egyre nehezebben lenne követhető. Köszönöm tehát a türelmes Olvasónak, hogy elkísért engem a radartechnika felfedezésére indított egyesztendős „kalandtúrámra”.
LÁBJEGYZETEK:
[1] Érdekes dolgok történnek, ha a hangforrás sebessége meghaladja a hullámnak a közeghez mért terjedési sebességét, azaz a forrás „lehagyja” a hullámfrontot. Ha a forrás például egy dalt játszik, és közben a terjedési sebességnek pontosan a kétszeresével mozog, a nyugvó megfigyelő normál hangmagassággal hallja a dalt – de visszafelé. A bizarrul hangzó, de könnyen belátható következtetést Lord Rayleigh brit fizikus írta le először (Nobel-díjas, de nem ezért kapta  )
)
[2]FFT: Fast Fourier Transform. Olyan numerikus eljárás, amely az időfüggvényből vett periodikus mintasorozatból számítja ki a frekvenciaspektrum mintavételezett képét. Az FFT az általános diszkrét Fourier-transzformáció (DFT) egy gyors kiszámíthatóságra optimalizált változata.
[3]Az ábrák arányai az áttekinthetőség érdekében torzítottak.
Készítette Tóth Ferenc
a www.radartutorial.eu weblap (szerző: Christian Wolff) fordításával, átdolgozásával és bővítésével a GNU Free Documentation License és a Creative Commons „Nevezd meg – Így add tovább 4.0” licence alapján.
A cikksorozat korábbi részei:
1. rész |
2. rész |
3. rész |
4. rész |
5. rész |
6. rész |
7. rész |
8. rész | 9. rész |